In 2016, the SAT and ACT tests were redesigned. (They used to be more different from each other than they are now.)
The A in the acronyms has not changed however:
- A in ACT means “achievement”
- A in SAT means “aptitude”
Before the 2016 redesigns, the distinction between an “achievement” question and an “aptitude” question was more
pronounced. Achievement questions tested, in a more straight-forward way, what students had achieved by learning and
understanding concepts from their math classes directly. Aptitude questions, on the other hand, did the same but also
tested the aptitude a student has for mathematical or analytic thinking.
Aptitude questions are probing a student’s ability to:
- Think creatively about a problem
- Think outside the box
- See patterns
- Solve puzzles
- Build models for the problem that can then be analyzed towards a solution
- Develop a methodology for solving a problem
In general, aptitude questions examine more creative problem solving skills.
Not to generalize, but students who tend to do better on these aptitude questions are the
chess playing, Rubik cube solving, analytically clever students. (We still call these students “nerds” but now
it is considered more of a compliment.)
Here is an example of the type of reasoning an aptitude type question is probing …
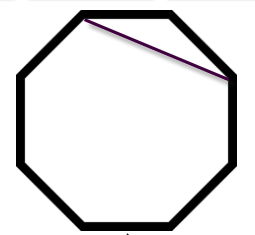
Problem: The octagon below shows only one diagonal drawn between a pair of vertices (diagonals are not sides). How many diagonals can be drawn between all the pairs of vertices?
Before reading on, try this problem yourself. See how many diagonals you can identify.
Solution 1:
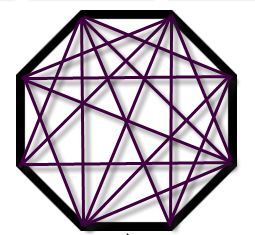
One approach would be to randomly draw all the diagonals and hope to draw them all and not duplicate any.
This is a somewhat random, haphazard approach, easily producing an incorrect answer.
For example, it might not be easy to realize that this solution is missing two diagonals:
Solution 2:
A better, more analytical, approach involves higher level aptitude and a methodology for getting to a solution.
Step-by-step solution:
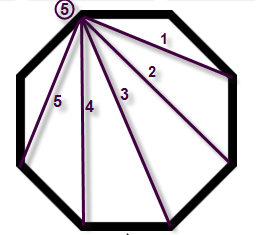
1) Select a vertex and exhaust all diagonals that start from there. Note how many diagonals by circling the number near the vertex being examined:
2) Move clockwise to the next vertex and draw all diagonals that start from there. Again, note the number in a circle near that vertex:
3) Once again, move clockwise to the third vertex, and drawn diagonals from there, taking care not to duplicate any. Note
the number of them near that vertex. This pictures shows that there are only four diagonals drawn from the third vertex.
4) Repeat once more and see that the 4th vertex has only three diagonals drawn from there, and a pattern emerges. Looks like from now on there will be one less diagonal drawn.
5) Do the next vertex and verify the observation that, indeed, one less diagonal can be drawn from there.
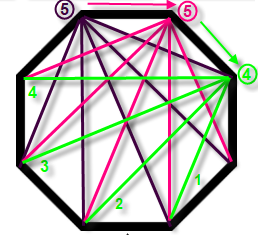
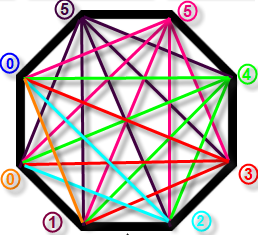
6) Continue clockwise until diagonals are drawn from all the vertices:
7) Add all the circled numbers for a solution of 20.
Note the following advantages to this more analytical approach:
- As you move around the polygon, the circled numbers act as checks that you are getting the number of diagonals correct. (The
circled numbers provide a real-time self-check.) - You are systematically (not randomly) drawing the diagonals, so you have a better chance of identifying them all
and not duplicating any.
Conclusion:
You have just seem an example of one of the higher level aptitude skills being tested in the SAT. Rather than a random
solution, the student has to devise a system or methodology to determine the solution.
The SAT is now closer to the ACT (after the 2016) design, so the aptitude testing aspect of the SAT
is not as prevalent as it once was. However, many aptitude testing questions still remain; so think like a nerd:
Think outside the box. Looks for patterns. Model the problem. Think creatively.
John Accardi
AcademicTestingAdvantage.com